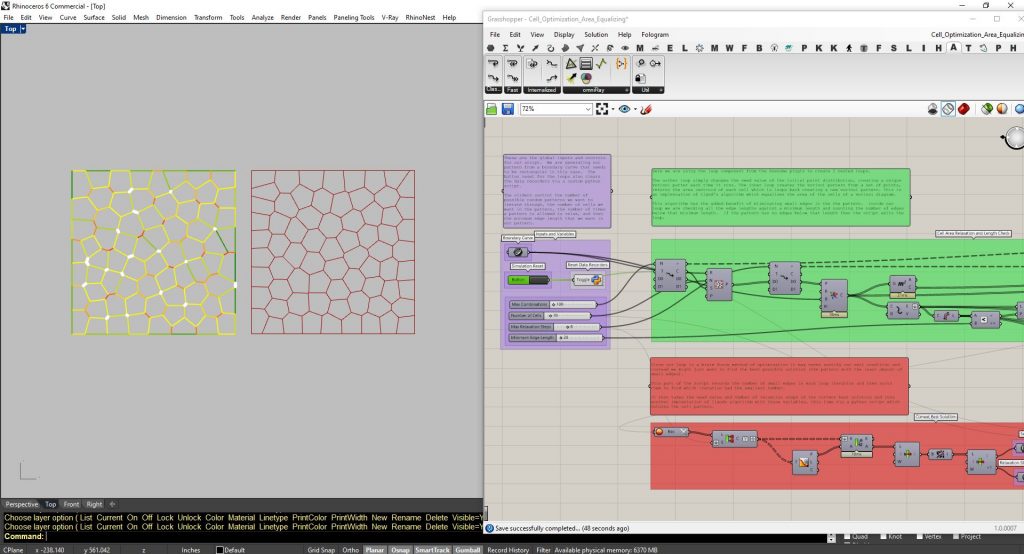
We spend a lot of time optimizing our designs for fabrication.  Normally this rationalization comes toward the end stages of the design process but a lot of time and energy can be saved if designs are rationalized from the beginning.

Vorinoi patterns can be a great tool for creating distributions and patterns like our project at One State Street.    They tend to produce a lot of small edges though which can be problematic for production when you start to introduce things like material thickness and fasteners.

This grasshopper definition is something we developed to help us start from an already optimized 2D vorinoi pattern.  Essentially it is an implementation of Llyods algorithm which performs iterative area optimization on the cells of a vorinoi diagram.  A side effect of this algorithm Is that it reduces the number of small edges. 

We took this algorithm and wrapped it in a loop that essentially lets us run through thousands of unique patterns to find the best diagram possible for our conditions.  The definition requires a few plugins, Anenome (for looping in grasshopper), Python (for some custom components), and Human Tools (for custom display purposes).

Download the definition here: Cell_Optimization_Area_Equalizing.zip